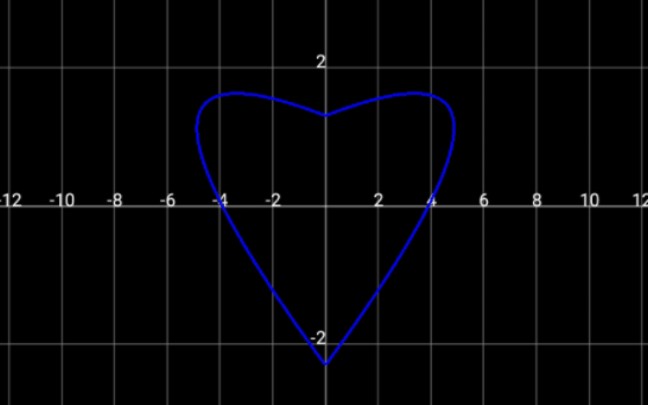
一、笛卡尔心形函数表达式是什么?
如下:
1、直角坐标方程
心形线的平面直角坐标系方程表达式分别为 :
x^2+y^2+a*x=a*sqrt(x^2+y^2) 。
x^2+y^2-a*x=a*sqrt(x^2+y^2)。
2、极坐标方程
水平方向: ρ=a(1-cosθ) 或 ρ=a(1+cosθ) (a>0)。
垂直方向: ρ=a(1-sinθ) 或 ρ=a(1+sinθ) (a>0)。
简介
笛卡尔在科学上的贡献是多方面的。笛卡尔不仅在哲学领域里开辟了一条新的道路,同时笛卡尔又是一勇于探索的科学家,在物理学、生理学等领域都有值得称道的创见,特别是在数学上他创立了解析几何,从而打开了近代数学的大门,在科学史上具有划时代的意义。
但他的哲学思想和方法论,在其一生活动中则占有更重要的地位。他的哲学思想对后来的哲学和科学的发展,产生了极大的影响。
二、笛卡尔心形函数的表达式是什么?
心脏可以极坐标的形式表示: r =a( 1 - sin θ)。方程为ρ(θ) = a(1 + cosθ)的心脏线的面积为:S=3(πa^2)/2。
心脏线,也称心形线,是外摆线的一种,亦为蚶线的一种,是一个圆上的固定一点在它绕着与其相切且半径相同的另外一个圆周滚动时所形成的轨迹,因其形状像心形而得名。
基本性质
1,a=1时的心脏线的周长为 8,围得的面积为3π/2。
2,心脏线亦为蚶线的一种。
3,在Mandelbrot set正中间的图形便是一个心脏线。
4,心脏线的英文名称“Cardioid”是 de Castillon 在 1741年 的《Philosophical Transactions of the Royal Society》发表的;意为“像心脏的”。