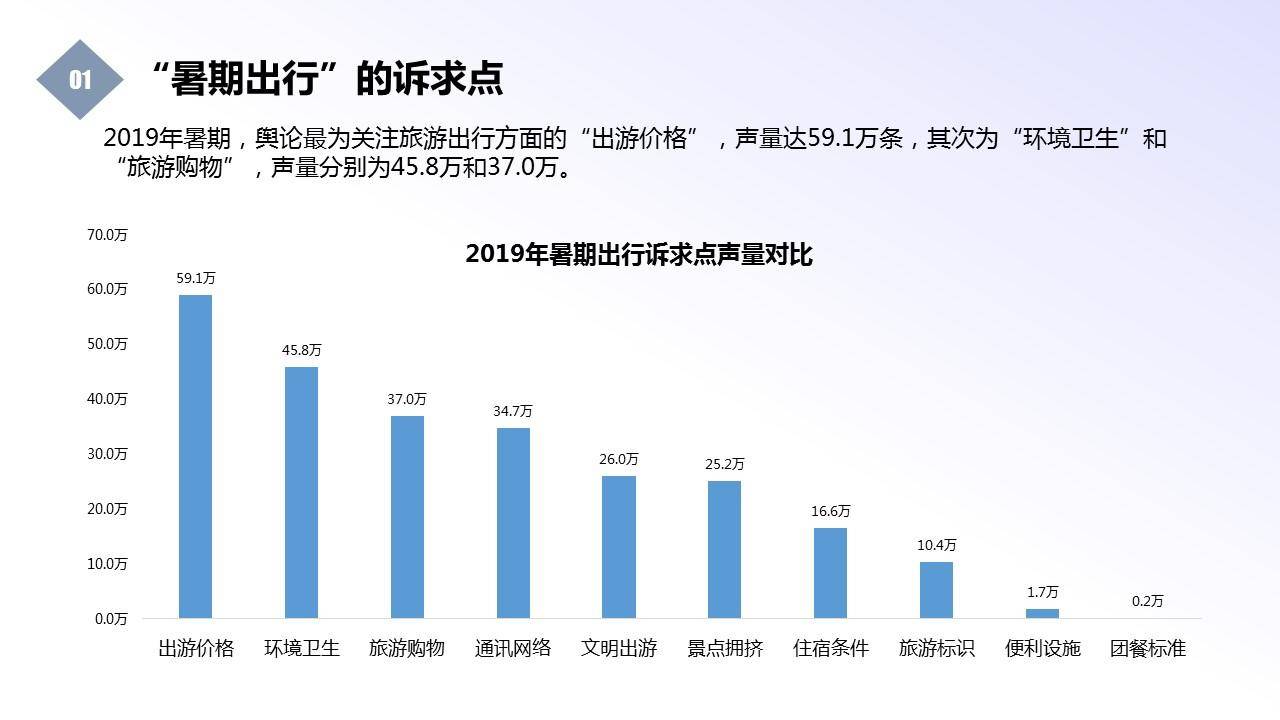
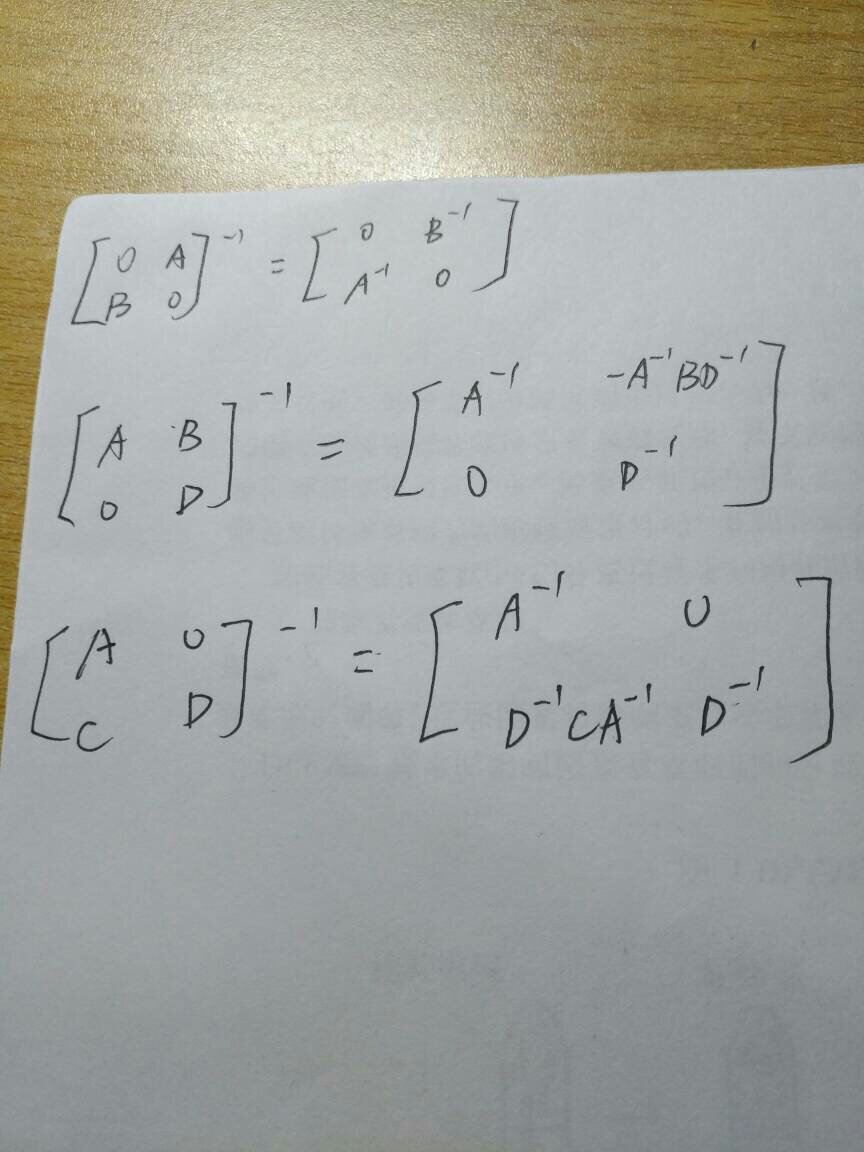一、逆矩阵怎么求?
计算公式:A^(-1)=(︱A︱)^(-1) A﹡(方阵A的行列式的倒数乘以A的伴随矩阵)。
这个公式在矩阵A的阶数很低的时候(比如不超过4阶)效率还是比较高的,但是对于阶数非常高的矩阵,通常我们通过对2n*n阶矩阵[A In]进行行初等变换,变换成矩阵[In B],于是橡碧B就是A的逆矩阵。
矩阵的乘法满足以下运算律:
结合律:
左分配律:
右分配律:
矩阵乘法不满足交换律。
扩展资料:
在线性代数中,相似矩阵是指存在相似关系的矩阵。相似关系是两个矩阵之间的一种等价关系。两个n×n矩阵A与B为相似矩阵当且仅当存在一个n×n的可逆矩阵P。
设 是数域, ,若存在 ,使得 , 为单位阵,则称 为可逆阵, 为 模历逆矩阵,记为 。若方阵 的逆阵存在,则称 为可逆矩阵或非奇异矩阵。
判断或证明 可逆的常用方法:
①证明 ;
②找一个同阶矩阵 ,验证 ;
③证明 的行向量(或列向量)线性无关。
假设M是一个m×n阶矩阵,旦如搜其中的元素全部属于域K,也就是实数域或复数域。如此则存在一个分解,其中U是m×m阶酉矩阵;Σ是m×n阶实数对角矩阵;而V*,即V的共轭转置,是n×n阶酉矩阵。
这样的分解就称作M的奇异值分解 。Σ对角线上的元素Σi,i即为M的奇异值。常见的做法是将奇异值由大而小排列。如此Σ便能由M唯一确定了。
二、逆矩阵怎么求?
逆矩阵的求法:
1、利用定义求逆矩阵
设A、B都是n阶方阵, 如果存在n阶方阵B 使得AB=BA=E, 则称A为可逆矩阵, 而称B为A的逆矩阵。
2、运用初等行变换法
将一n阶可逆矩阵A和n阶单位矩阵I写成一个nX2n的矩阵B=(A,I])对B施行初等行变换,即对A与I进笑扰行完全相同的若干初等行变换,目标是把A化为单位矩阵。当A化为单位矩阵I的同时,B的右一半矩阵同时化为了A的逆矩阵。
3、增广矩阵法
如果要求逆的矩阵是A,则对增广矩阵(A E)进行初等行变换,E是单位矩阵,将A化到E,此时此矩阵的逆就是原来E的位置上的那个矩阵,原理是 A逆乘以(A E)= (E A逆)初等行变换就是在矩阵的左边乘以A的逆矩阵得到的。
4、待定系数法
待定系数法顾名思义就是对未知数进行求解。用一个新的包含未定因子的多项式来表达多项式,从而获得一个恒等式。接着,利用恒等式的特性,推导出一碰槐旦类系数必须满足的方程或方程,再由方程组或方程组得到待确定的系数,或确定各系明埋数之间的对应关系,称为待定系数法。
三、求逆矩阵的方法
逆矩阵的求法有多种,其中重要的有伴随矩阵法、初等变换法和定义法等方法1。在使用伴随矩阵法求逆矩阵时,需要先判断矩阵是否可逆,即求矩阵的行列式是否不等于0。如果可逆,则可以按照以下步骤求逆矩阵2:1. 老塌求矩阵的代数余子式;2. 求伴随矩阵,即将代数余子式的转置形式作为矩阵;3. 得到逆矩阵,即将伴随矩阵除以矩阵的行列式。初等变换法求逆矩阵的思路是将原矩阵与单位矩阵拼接成一个大矩阵,然后通过一系列初等行变换将左边的矩阵变为单位矩阵,右边的矩阵就是所求的逆矩阵1。
逆矩阵的求法有多种,其中重要的有伴随矩阵法求逆矩阵,初等变换法求逆矩阵,以及定义法求逆矩阵,特殊矩阵求逆矩阵等方法,但是在求逆矩槐含模阵的时候,首先要判断该矩阵是否可逆,常用的方法有两种:
(1)定义法铅缓:若存在矩阵B,使得AB=E,则A可逆
(2)利用矩阵的可逆的判别条件:若则A可逆
下面介绍求A的逆矩阵的几种常用方法:
(一)伴随矩阵法
若n阶矩阵A可逆,则
在使用此方法的时候首先要判断矩阵A是否可逆,只需要求行列式不等于0就可逆.