一、直角三角形斜边公式

【直角三角形的斜边怎么求啊？】

计算公式-直角三角形斜长的计算 直角三角形斜边长度的计算，（一）已知两条直角边的长度，1）可按公式：c2=a2+b2 (2是平方)（二）如已知一条直边和一个锐角，可用直角三角函数计算直角三角形ABC的六个元素中除直角C外，其余五个元素有如下关系A+B=90度 SinA=角A的对边 / 斜边CosA=角A的邻边 / 斜边tgA=角A的对边 / 角A的邻边ctgA=角A的邻边 / 角A的对边例：角A等于30度，角A的对边是4米，计算斜边C是多少？查表sin30度=0.5,C=4/0.5=8三角函数值除了查表，也可以用电脑系统自带的计算器，计算.开始——程序——附件——计算器.这个计算器有两种模式，点‘查看’有一个下拉菜单，有标准型和科学型，选择科学型，输入度数后正弦点sin，余弦点cos，正切点tan，值就直接显示出来了.这里有一个度和度分秒转换的问题.如 18.69度，其中整数18就是18度，那么18.69-18=0.69，用0.69*60=41.4这里整数41就是41分，再41.4-41=0.4，再用0.4*60=24这个24就是秒.18.69度=18度41分24秒也可以用计算器直接转换：输入度数18.69——钩上Hyp——再点dms就显示出18.4124，这就是18度41分24秒.如要转换回去就输入18.4124——钩上Inv——再点dms，就转换了.有一点请注意，显示度分秒时，小数点后面是一位数或三位数如：15.3; 15.302，应读作15度30分；和15度30分20秒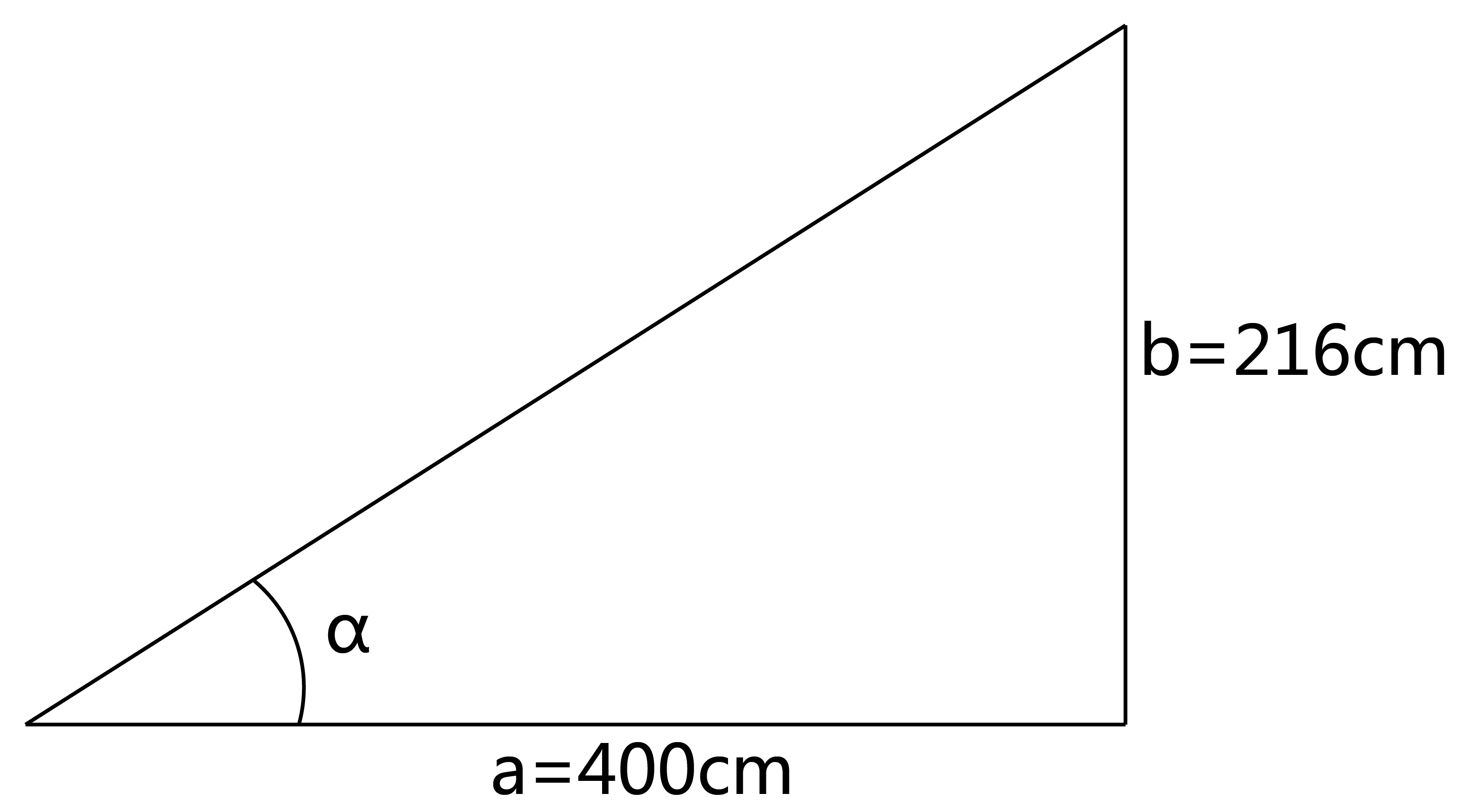

直角三角形已经知道两边长了,那么斜边该怎么算？

已知两条直角边a、b，求斜边c

勾股定理是a²+b²=c²（a、b是直角三角形的两条直角边，c是直角三角形的斜边）。

所以：c=√（a²+b²）

最后将两条直角边a、b数值代入即可求得斜边c。

扩展资料

由勾股定理到面积关系

如图，在Rt△ABC中， ∠ C=90°

AB=c,AC=b,BC=a，分别以a,b,c三边为边做正四边形，

那么有s2 + s3 = s1

证明：∵ s2 = b²，s3 = a²，s1 = c²

根据勾股定理：a²+b²=c²

∴ s2 + s3 = s1

三角形斜边计算公式

1、勾股定理：c^2=a^2+b^2

2、三角函数：c=a/cosB或c=b/cosA

c=a/sinA或c=b/sinB

（说明：斜边c，直角边a、b。与其对着的角分别为直角C，锐角A、B）

直角三角形的斜边的长度可以使用毕达哥拉斯定理找到，该定理表示斜边长度的平方等于另外两边长度的平方和。

例如，如果其中一方的长度为3（平方，9），另一方的长度为4（平方，16），那么它们的正方形加起来为25。斜边的长度为平方根25，即5。

扩展资料：

斜边的长度等于两个短边的正投影的长度之和。短边长度的平方等于其在斜边上的正投影长度乘以其长度的乘积。

斜边一定是直角三角形的三条边中最长的；斜边所对应的那条高是直角三角形的三条边中最短的；在直角三角形中，两条直角边的平方和等于斜边的平方（也称勾股定理）。

若一个三角形的两条直角边的平方和等于斜边的平方，那么这个三角形一定是直角三角形（称勾股定理的逆定理）。

二、30度直角三角形勾股定理公式

30度直角三角形勾股定理公式a²+3a²=4a²。

假设30度的对边是a，那么斜边就是2a。由此可得30度直角三角形勾股定理公式a²+3a²=4a²。

直角三角形的性质：

1、直角三角形两直角边的平方和等于斜边的平方。

2、在直角三角形中，两个锐角互余。

3、直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。该性质称为直角三角形斜边中线定理。

4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。

三、30度的直角三角形，斜边怎么算？👀👀

若已知这个直角三角形的一个直角边，求斜边，如图，直角边是a、b，斜边是c，则:

c=a/sin30º

或c=b/cos30º

四、有30度角的直角三角形，已知一直角边，求另两边的公式，快速求法

求解方法分析过程如下：

有30度角的直角三角形，已知一直角边，如下图所示：

根据在直角三角形中，30度所对的直角边是斜边的一半可得斜边=2a。根据勾股定理可得另一直角边是√3a。

如果知道的是30度的邻直角边，则30度所对的直角边是30度的邻直角边÷√3。斜边再根据30度所对的直角边是斜边的一半，求解。

扩展资料：

直角三角形的性质：

1、直角三角形两直角边的平方和等于斜边的平方。

2、在直角三角形中，两个锐角互余。

3、直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。该性质称为直角三角形斜边中线定理。

4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。

5、在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。

五、30直角三角形边长怎么算

邻边为30cm由30度可知，斜边=30*根号3分之二=20倍根号3对边=斜边/2=10倍根号3。

应用勾股定理：斜边平方=两直角边平方之和

例如，对于任意一直角三角形而言，设两直角边长度分别为a和b，斜边长为c，则根据勾股定理可得到公式：a²+b²=c²

对于题中的直角三角形来说，利用勾股定理可得：斜边=√(2.36²+1.2²)=√7.0096≈2.648

勾股定理

中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

在中国，商朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。