一、分部积分法公式例题是什么?
分部积分法公式是∫ u'v dx = uv - ∫ uv' dx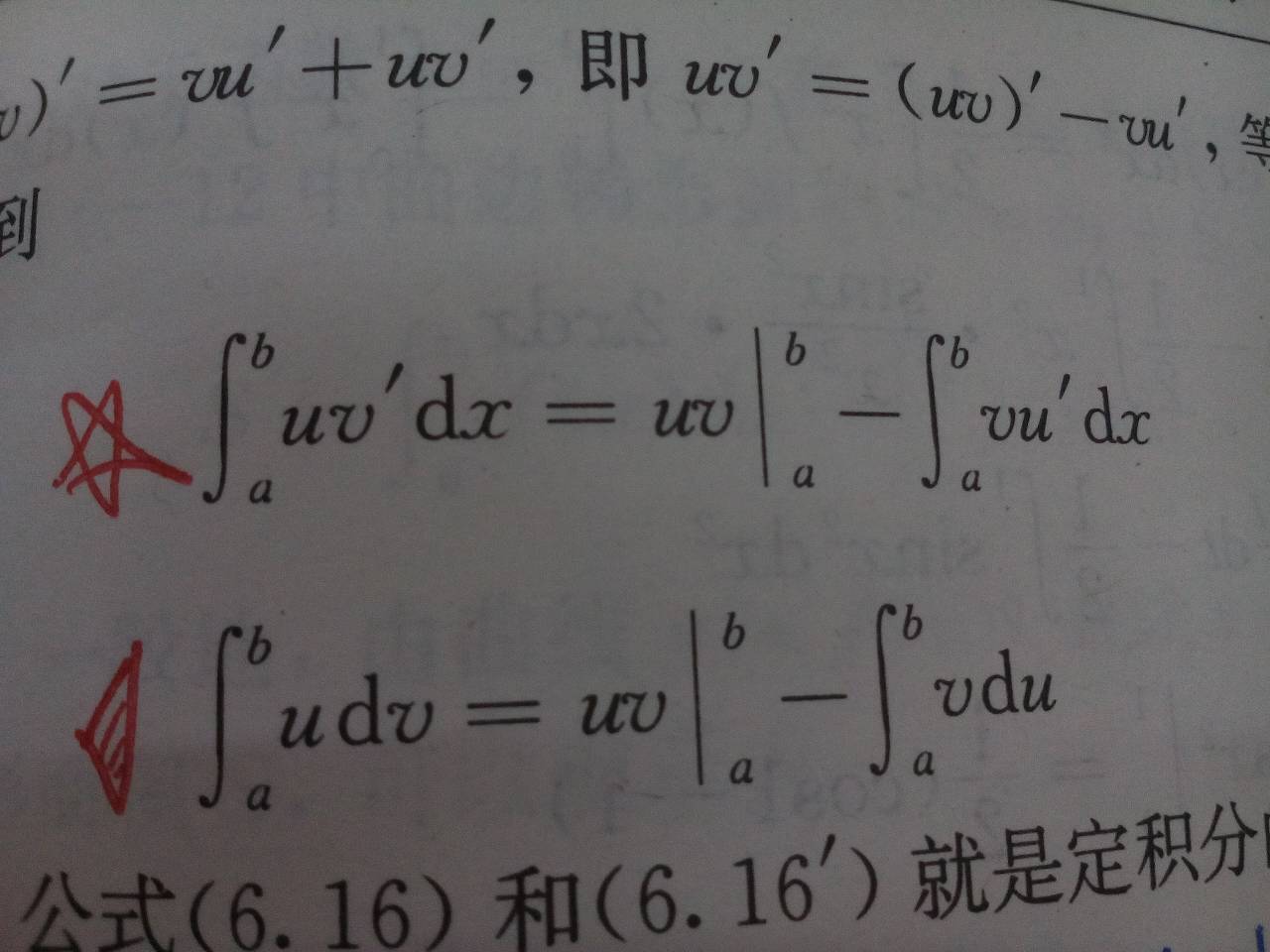
定理1:设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
定理2:设f(x)区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
定理3:设f(x)在区间[a,b]上单调,则f(x)在[a,b]上可积。
黎曼积分:
定积分的正式名称是黎曼积分。用黎曼自己的话来说,就是把直角坐标系上的函数的图象用平行于y轴的直线把其分割成无数个矩形,然后把某个区间[a,b]上的矩形累加起来,所得到的就是这个函数的图象在区间[a,b]的面积。实际上,定积分的上下限就是区间的两个端点a,b。
二、分部积分公式是什么?
分部积分公式:∫u'vdx=uv-∫uv'dx。
分部积分:
(uv)'=u'v+uv'
得:u'v=(uv)'-uv'
两边积分得:∫u'vdx=∫(uv)'dx-∫uv'dx。
即:∫u'vdx=uv-∫uv'dx,这就是分部积分公式,也可简写为:∫vdu=uv-∫udv。
积分基本公式
1、∫0dx=c
2、∫x^udx=(x^u+1)/(u+1)+c
3、∫1/xdx=ln|x|+c
4、∫a^xdx=(a^x)/lna+c
5、∫e^xdx=e^x+c
6、∫sinxdx=-cosx+c
7、∫cosxdx=sinx+c
8、∫1/(cosx)^2dx=tanx+c
9、∫1/(sinx)^2dx=-cotx+c