一、双曲线准线的方程
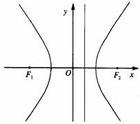
双曲线有两条准线L1(左准线),L2(右准线),准线与双曲线的位置关系如右图所察芦圆示。
以原点为中心的双曲线 的准线的方程就是:x=±a²哗局/c;
以原点为中心的双曲线 的准线的方程就是:y=±a²/c;
其中a是实半轴长,b是虚半轴长,c是半焦距。( )
例如,存在以原点为中心的双曲线 按照以上计算公式,则其准线方程为:
L1的方程: ;败塌L2的方程: 。
二、双曲线的准线方程
对于双曲线来说,与左焦点f1(-c,0)对应的准线叫做左准线,其方程为x=-a^2/c;与右焦点困段f2(c,0)对芦缺应的准线叫做右准线,其方程为x=a^2/c。汪哗誉
三、双曲线准线方程
双曲线是一种常见的二次曲线,其准线是指其两个分支的渐近线,即双曲线的两个分支趋近于准线而无限延伸。双曲线闭渗准线方程可以通过以下步骤推导得耐态配出:
1. 假设双曲线的方程为:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,其中$a$和$b$为正实数。
2. 将双曲线方程化简为标准形式:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \Rightarrow \frac{x^2}{a^2}-1=\frac{y^2}{b^2}$。
3. 求出双曲线的渐近线斜率:$m=\pm \frac{b}{a}$。
4. 根据斜率和双曲线的中心点坐标,得出双曲线的两条渐近线方程:
- 对于双曲线的左右分支,渐近线方程为:$y=\pm \frac{b}{a}x$。
- 对于双曲线的上下分支,渐近线方程为:$x=\pm \frac{a}{b}y$。
因此,双曲线准线方程就是双曲线的渐近线方程,即:
- 对于双曲线的左右分支,准线方程为:昌指$y=\pm \frac{b}{a}x$。
- 对于双曲线的上下分支,准线方程为:$x=\pm \frac{a}{b}y$。
这就是双曲线准线方程的推导过程。在实际应用中,双曲线准线方程可以用于确定双曲线的形状和位置,以及计算双曲线的各种参数。
四、双曲线的标准方程
双曲线的标准方程如下:
标准方程1:焦点在X轴上时为x2/a2-y2/b2=1(a>0,b>0)。
标准方程1:焦点在Y轴上时为y2/a2-x2/b2=1(a>0,b>0)。
双曲线取值范围厅宏宽:│x│≥a(焦点在x轴上)或者│y│≥a(焦点在y轴上)。
双曲线对称性:关于坐标轴和原点对称,其中扮亮关于原点成中心对称。
双曲线的定义:
(1)平面内,到两个定点的距离之差的绝对值为常数(小于这两个定点间的距离)的点的轨迹称为双曲线。定点叫双曲线的焦点。
(2)平面内,到给定一点及一直线的距离之比为常数e(e=c/a(e>1),即为双曲线的离心率)的点的轨迹称为双曲线。定点叫双曲线的焦点,定直线叫双曲线的准线。双曲线准线的方程为x=±a²/c(焦点在x轴上)或y=±a²/c(焦点在y轴上)。
(3)一平面截一圆锥面,当截面绝伏与圆锥面的母线不平行,且与圆锥面的两个圆锥都相交时,交线称为双曲线。
以上内容参考:百度百科-双曲线的标准方程
五、双曲线的准线方程公式
双曲线的准线方程公式:x^2/a^2-y^2/b^2=1。平慎如面内到一个定点与一条定直线的距离之比是一个大于1的常数的动点的轨迹是双曲线,这个常数即该双曲线的离心率,定点是双曲线的焦点,定直线是双曲线的准线。
一般的,双曲线是定义为平面交截直角圆锥面的两半的一类圆纯册锥曲线。它还可以定义为与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。这个固定的距离差是a的两倍,这里的做孝宏a是从双曲线的中心到双曲线最近的分支的顶点的距离。a还叫做双曲线的实半轴。焦点位于贯穿轴上,它们的中间点叫做中心,中心一般位于原点处。